1) неравенство f(y0)<0 является достаточным условием существования максимума в точке у0;

2) неравенство / (i/0) > 0 является достаточным условием существования минимума в точке у0.

Если же для функции одной переменной / (у0) = 0, то необходимо исследовать производные высших порядков в соответствии со следующей теоремой.

Теорема 20.1.3. Если в стационарной точке уй функции f(y) первые (п- 1) ее производных равны нулю и f \у0) * 0, то в точке у = у0 функция f(y) имеет

1) точку перегиба, если п - нечетное;

2) точку максимума, если п - четное и fM(y0) < 0;

3) точку минимума, если п - четное и f in\y0) > 0.

Пример 20.1.3

Рассмотрим функцииДу) = у* п g(y) = у3. Для функцииду) =у4 имеем

/(у) -4/ = 0,

откуда получаем стационарную точкуу0 = 0. Далее находим

/(О) =/ (0) =/,3,(0) = 0. Так какfi4\0) = 24 > 0, тоу0 = 0 является точкой минимума (рис. 20.2). Для функции g(y) = у3 имеем

g(y)=3y2 = 0.

Следовательно, точка у0 = 0 является стационарной точкой. Поскольку g(0) =g (0) = 0, g<3)(0) = 6 и не обращается в нуль, точкау0 = 0 является точкой перегиба.

/О) /у4

Рис. 20.2. Стационарные точки функций i(y) = у и g(y) = у

УПРАЖНЕНИЯ 20.1.1

1. Найдите экстремальные точки следующих функций.

a) f(x) = х3 + х.

b) /(*) = х* + х2.

c) f(x) = 4х4 - х2 + 5.

d) /(*) = (Зх - 2)\2х - 3)\

e) f(x) = 6xs-4x3 + 10.

2. Найдите экстремальные точки следующих функций.

a) /(X) = х3 + xl - Зх,х2.

b) f(X) = 2xf +xj и-*2 + 6(х, + х2 + х}) + 2х1х2х1.

3. Проверьте, что функция

/ (х х2, х,) = 2x1x2xJ - 4хххг - 2х2х, + х* + х\ + х2 - 2xt - 4х2 + 4х,

имеет стационарные точки (0, 3, 1), (0, 1, -1), (1, 2, 0), (2, 1, 1) и (2, 3, -1). Используйте достаточные условия для нахождения экстремумов функции.

4. Решите следующую систему уравнений путем превращения ее в задачу минимизации нелинейной целевой функции при отсутствии ограничений на переменные.

х2 - xf = 0 , хг - хх = 2.

(Подсказка, min / \xv х2) имеет место при /(* хг) = 0.)

5. Докажите теорему 20.1.3.

20.1.2. Метод Ньютона-Рафсона

В общем случае использование необходимого условия экстремума V/(X) = 0 для поиска стационарных точек функции /(X) может быть сопряжено с трудностями, возникающими при численном решении соответствующей системы уравнений. Метод Ньютона-Рафсона предлагает итерационную процедуру решения системы нелинейных уравнений. Несмотря на то что данный метод рассматривается в этом разделе именно в указанном контексте, на самом деле он относится к числу градиентных методов численного поиска экстремумов функций при отсутствии ограничений (см. раздел 21.1.2).

Рассмотрим систему уравнений

/,(Х) = 0,£=1,2, ...,т. Пусть X* - некоторая фиксированная точка. Используя разложение Тейлора, имеем /((Х) * /,(Х*) + V/,(Xk)(X - X*), i - 1, 2, т.

Следовательно, исходная система уравнений приближенно представима в виде

/,(Х*) + V/,(X)(X - X*) = 0, i = 1, 2.....т.

Эти уравнения можно записать в матричной форме:

Ак + ВДХ-Х*) = 0.

Предположим, что векторы /,(Х) независимы, тогда матрица В, является невырожденной. В результате из предыдущего уравнения получим

х = х-в;Ч,.

Идея метода Ньютона-Рафсона состоит в следующем. На первом шаге выбирается начальная точка Х°. С помощью полученного уравнения по известной точке X* можно вычислить координаты новой точки X**1. Процесс вычислений завершается в точке X , которая считается приближенным решением исходной системы, если Xm X 1.

Геометрическая интерпретация данного метода для функции одной переменной f(x) приведена на рис. 20.3. Связь между точками хк и х*+1 в этом случае выражается формулой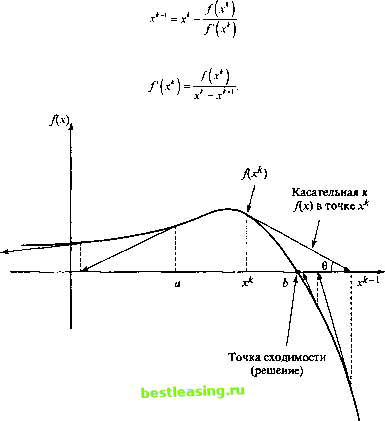

Рис. 20,3. Итерационный процесс в методе Нъютона-Рафсона

На рис. 20.3 видно, что положение точки хк+1 определяется углом 0 наклона касательной к графику функции f(x) в точке хк, где tg0= fix ).

Одним из недостатков изложенного метода является то, что для функций общего вида не всегда гарантируется его сходимость. На рис. 20.3 видно, что при выборе в качестве х° точки а итерационный процесс расходится. Простых рецептов для выбора хорошего начального приближения не существует.

Пример 20.1.3

Для демонстрации работы метода Ньютона-Рафсона рассмотрим задачу нахождения стационарных точек функции

f{x) = (Зх - 2)\2х - З)2.

Чтобы найти стационарные точки, надо решить уравнение f(x) = 0, которое в данном случае принимает вид кубического уравнения

72х3 - 234х2 + 241х - 78 = 0.