Шаблон Excel ch20NewtonRaphson.xls методом Ньютона-Рафсона может решить любое уравнение с одной переменной. На рис. 20.4 показано решение в этом шаблоне уравнения данного примера. Чтобы найти это решение, надо в ячейку СЗ ввести следующее выражение, заменив переменную х ссылкой на ячейку A3.

72л3 - 234л:2 + 24 Ьс -78 216х2-468л-+ 241

Отметим, что числитель этого выражения является формулой для вычисления первой производной функции f(x), а знаменатель - формулой второй производной, что и требуется для метода Ньютона-Рафсона при решении уравнения f(x) = 0. Перед началом вычислений также задается предел точности А (= 0,001) и начальное значение х0 (= 10). Если разность между значениями хь и Xм будет меньше предела точности, то процесс вычислений завершается. В данном примере метод сошелся к значению х = 1,5.

Рис. 20.4. Решение алгебраического уравнения методом Ньютона-Рафсона

На самом деле наша функция f(x) имеет три стационарные точки х = 2/3, х = 13/12 и х = 3/2. Оставшиеся две стационарные точки можно найти, если задать соответствующие начальные значения, например, л:0 = 0,5 и х0= 1. В общем случае надо сделать несколько попыток решения задачи методом Ньютона-Рафсона при различных начальных значениях, чтобы отыскать все корни уравнения. В данном примере нам повезло - мы знаем, что наше уравнение имеет три корня. Однако в случае сложных уравнений или уравнений, зависящих от нескольких переменных, как правило неизвестно ни количество корней, ни их местоположение.

УПРАЖНЕНИЕ 20.1.2

1. Примените метод Ньютона-Рафсона для решения упражнений 20.1.1.1, с и 20.1.1.2, Ъ.

20.2. ЗАДАЧИ НА ЭКСТРЕМУМ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ

В настоящем разделе рассматриваются задачи поиска экстремумов непрерывных функций при наличии ограничений на переменные. В разделе 20.2.1 рассматривается ситуация, когда дополнительные ограничения имеют вид равенств, а в разделе 20.2.2 - неравенств. Основная часть материала раздела 20.2.1 изложена в соответствии с [2].

20.2.1. Ограничения в виде равенств

В данном разделе рассматривается два метода решения оптимизационных задач при наличии ограничений в виде равенств: метод Якоби и метод Лагранжа. Метод Лагранжа можно логически получить из метода Якоби. Эта связь позволяет дать интересную экономическую интерпретацию метода множителей Лагранжа.

Метод приведенного градиента (метод Якоби). Рассмотрим задачу

минимизировать z = /(X)

при ограничениях

g(X) = 0,

X = (дг х2, дсл),

S (.§!> &2> *

Функции /(X) и g,(X), t= 1, 2, т, предполагаются дважды непрерывно дифференцируемыми.

Идея использования приведенного градиента заключается в том, чтобы найти замкнутое аналитическое выражение для первых частных производных функции /(X) во всех точках, удовлетворяющих ограничениям g(X) = 0. Соответствующие стационарные точки определяются из условия равенства нулю указанных частных производных. Затем можно использовать достаточные условия, сформулированные в разделе 20.1, для классификации найденных стационарных точек.

Для пояснения изложенной идеи рассмотрим функцию /(дг х2), график которой представлен на рис. 20.5. Предположим, что эту функцию необходимо минимизировать при ограничении

g,(*i. х2) = х2 - Ь = 0,

где Ь - некоторая константа. На рис. 20.5 видно, что кривая, которая проходит через точки А, В и С, состоит из значений функции /(дг х2), для которых заданное ограничение выполнено. В соответствии с рассматриваемым методом определяются компоненты приведенного градиента функции /(дг х2) в каждой точке кривой ABC. Точка В, в которой приведенная производная обращается в нуль, является стационарной для рассматриваемой задачи с ограничением.

Теперь рассмотрим общую математическую формулировку метода. Из теоремы Тейлора следует, что для точек X + АХ из окрестности точки X имеем

/(х+дх)-/(х) = у/-(х)дх+о(дх,2),

g(X + AX)-g(X) = Vg(X)AX + 0(Ax2).

Лх{,х2)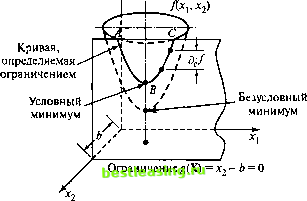

Рис. 20.5. Иллюстрация к методу Якоби

При hxj - 0 эти уравнения принимают вид

d/(X) = V/(X)c5X,

dg(X) = vg(X)ax.

Поскольку g(X) = 0, 9g(X) = 0 в допустимой области. Отсюда следует, что

о/(Х) - V/(X)3X = 0,

vg(x>ax = o.

Как видим, задача сводится к решению т + 1 уравнений с п + 1 неизвестными, которыми являются 9/(Х) и ЭХ. Неизвестную величину 9/(Х) можно определить, как только будет найден вектор 5Х. Это означает, что, по существу, имеется т уравнений с п неизвестными.

При т > п по меньшей мере т- п уравнений системы являются избыточными. После устранения избыточности количество независимых уравнений в системе становится равным т (< п). Если т = п, решением является ЭХ = 0. При этом точка X не имеет допустимой окрестности, и, следовательно, пространство решений задачи состоит из единственной точки. Такая ситуация является тривиальной. Ситуацию, когдат<п, рассмотрим подробно.

Пусть X = (Y, Z), где

Y = (j/p уг, ...,ym)nZ = (z1,z2, ...,zn m)