случаях, когда задача имеет единственное оптимальное решение. Другим важным моментом является ошибочность интуитивного представления, что если p<q, то оптимальное значение целевой функции /(X) при р ограничениях-равенствах всегда лучше, чем при q ограничениях-равенствах. В общем случае это имеет место лишь в том случае, когда набор из р ограничений является подмножеством набора из q ограничений. Рассматриваемый ниже пример служит иллюстрацией сказанного.

Пример 20.2.6

при ограничениях

Максимизировать z = - (2.x, - 5 )2 - (2дг2 -1 )2

х, + 2х2 < 2, хх,хг>0.

Графическое представление данной задачи (рис. 20.7) призвано помочь в понимании аналитических выкладок. Как видим, целевая функция задачи является вогнутой, а область допустимых решений выпуклой. Отсюда следует, что эффективный алгоритм должен гарантировать определение глобального оптимума. Однако обобщенный метод множителей Лагранжа, как будет показано, позволяет найти лишь точку локального максимума.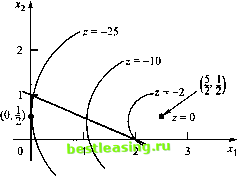

Рис. 20.7. Пространство решений для задачи примера 20.2.6

Точка безусловного экстремума находится как решение уравнений

- =-4(2*.-5) = 0,

дх, У 1

= (2x2-l) = 0.

Отсюда имеем (xv х2) = (5/2, 1/2). Так как это решение не удовлетворяет условию .г, + 2лг2 < 2, ограничения поочередно активизируются. Рассмотрим ограничение х, = 0. Функция Лагранжа в этом случае примет вид

L(x x2,\) = -(2x, - 5)2 -(2дг2 -I)2 -Хх{.

Следовательно,

-4(2jc,-5

)-к = 0,

-4(2х2-1) = 0,

-х, = 0.

Решением этой системы будет точка (х х2) = (0, 1/2), которая является точкой максимума, в чем можно убедиться, используя достаточное условие. Поскольку эта точка удовлетворяет остальным ограничениям исходной задачи, вычислительная процедура завершается: (х1,х2) = (0, 1/2) - точка локального максимума задачи. (Заметим, что если поочередно активизировать оставшиеся ограничения задачи хг > 0 и х, + 2х2 < 2, то получаются недопустимые решения.) Оптимальное значение целевой функции z = -25.

Как видно из рис. 20.7, допустимому решению (х х2) = (2, 0) рассматриваемой задачи, которое определяется точкой пересечения двух прямых х2 = 0 и х, + 2х2 = 2, соответствует значение целевой функции z = -2. Оно лучше значения функции z, которое получено с учетом одного активного ограничения.

Как следует из описанной вычислительной процедуры, при реализации обобщенного метода множителей Лагранжа на большее, чем получение приемлемого допустимого решения задачи, не следует рассчитывать. Особенно это проявляется тогда, когда целевая функция задачи не является одновершинной. Если в оптимизационной задаче имеется единственный (глобальный) условный экстремум (как в примере 20.2.6), то, чтобы его найти, можно использовать откорректированный обобщенный метод множителей Лагранжа. Для этого необходимо провести сравнение безусловного оптимума и условных экстремумов, полученных с учетом всех возможных наборов активных ограничений, т.е. когда сначала отдельные ограничения делаются активными поочередно, затем рассматриваются пары активных ограничений, и так до тех пор, пока все т ограничений рассматриваемой задачи не станут активными. Наилучший из всех таких допустимых экстремумов является глобальным.

Если эту процедуру применить к решению задачи из примера 20.2.6, то для определения глобального экстремума необходимо решить семь задач. Это свидетельствует о том, что возможности использования обобщенного метода множителей Лагранжа для решения практических задач ограничены.

Условия Куна-Таккера. Данный раздел посвящен рассмотрению необходимых условий Куна-Таккера, которые позволяют определять стационарные точки в задаче нелинейного программирования с ограничениями в виде неравенств. В основу изложения положен метод множителей Лагранжа. Эти условия являются также и достаточными, если выполняются определенные правила, которые описаны ниже.

Рассмотрим следующую задачу.

Максимизировать г = ДХ)

g(X)<0.

Ограничения-неравенства можно преобразовать в равенства с помощью неотрицательных дополнительных переменных. Пусть Sf[>Q) - дополнительная переменная, которая прибавляется к левой части t-ro ограничения gt(X.) < 0 и пусть

S = (S S1,...,S\T и S2 =(S12,S22,...,5)r,

где т - общее количество ограничений-неравенств. Следовательно, функция Лагранжа записывается в виде

ДХ, S,X) = /(X)-X[g(X) + S2].

При ограничениях g(X) < 0 необходимым условием оптимальности в задаче максимизации (минимизации) является неотрицательность (соответственно, неположительность) множителей X. Приведем обоснование этого. Рассмотрим задачу максимизации. Так как множители X выражают скорость изменения целевой функции / по отношению к изменениям g, т.е.

то как только правая часть ограничения g(X) < 0 увеличивается и становится больше нуля, область допустимых решений задачи расширяется и, следовательно, оптимальное значение целевой функции не может уменьшиться. Это значит, что X > 0. Аналогично в задаче минимизации при увеличении правой части ограничения оптимальное значение функции / не может увеличиться, откуда следует, что X < 0. Если же ограничения задачи имеют вид равенств, т.е. g(X) = 0, то компоненты вектора X по знаку не ограничены (см. упражнение 20.2.4.2).

Указанные выше ограничения на вектор X должны рассматриваться как часть необходимых условий Куна-Таккера. Теперь получим остальные условия.

Вычисляя частные производные функции L по X, S и X и приравнивая их к нулю, получаем

l = V/(X)-Wg(X) = 0,

- = -2XS = 0, ; = 1, 2,...,/я,

dS,

Из второй группы уравнений следуют такие результаты.

1. Если Я, не равняется нулю, то S2 = 0 . Это означает, что соответствующий этому ограничению ресурс является дефицитным и, следовательно, полностью исчерпан (ограничение имеет вид равенства).

2. Если S2 > 0 , то Я, = 0. Это значит, что i-й ресурс дефицитным не является и, следовательно, не влияет на значение целевой функции/(т.е. Х,=-- = 0).

Из второй и третьей групп уравнений следует, что

Яд(Х) = 0, i=l,2, ...,т.