3. Запишите необходимые условия Куна-Таккера для следующих задач.

a) Максимизировать /(X) = х3 -xl + х,х2

при ограничениях

х, + xj + х, = 5, 5х2 - xl - хъ > 0, х,>0, х2>0, х3>0.

b) Минимизировать /(X) = х4 + х22 + 5х,;с2х,

при ограничениях

*2-x2+.x33 <10, х, +х22+4д:220.

4. Дана задача

максимизировать ДХ)

при ограничениях

g(X) = 0.

Пусть ДХ) - вогнутая функция, а g,(X) (t = 1, 2, т) - линейные функции. Покажите, что в этом случае необходимые условия Куна-Таккера оказываются также и достаточными. Верно ли последнее утверждение, если ёДХ) является выпуклой нелинейной функцией для всех г? Почему?

5. Дана задача

максимизировать /(X)

при ограничениях

gi(X)>0,g2(X) = 0,g3(X)<0.

Сформулируйте условия Куна-Таккера для данной задачи и установите требования к функциям, при реализации которых выполняются указанные условия.

ЛИТЕРАТУРА

1. Bazaraa М., Shrali Н. and Shetty С. Nonlinear Programming Theory and Algorithms, 2nd ed., Wiley, New York, 1993. (Существует перевод первого издания: Базара М., Шетти К. Нелинейное программирование. Теория и алгоритмы. - М.:Мир, 1982.)

2. Beightler С, Phillips D. and Wilde D. Foundations of Optimization, 2nd ed., Prentice Hall, N. J., 1979.

3. Rardin R. Optimization in Operations Research, Prentice Hall, N. J., 1998.

Литература, добавленная при переводе

1. Банди Б. Методы оптимизации. Вводный курс. - М.: Радио и связь, 1988.

2. Зангвилл У. И. Нелинейное программирование. - М.: Сов. радио, 1973.

3. Сухарев А. Г., Тимохов А. В., Федоров В. В. Курс методов оптимизации. - М.: Наука, 1986.

4. Поляк Б. Т. Введение в оптимизацию. - М.: Наука, 1983.

5. Химмельблау Д. Прикладное нелинейное программирование. - М.: Мир, 1975.

ГЛАВА 21

АЛГОРИТМЫ НЕЛИНЕЙНОГО ПРО ГРАМ М И РО В АН ИЯ

Методы решения задач нелинейной программирования условно можно разделить на два класса: прямые и непрямые методы. Примером прямых методов могут служить градиентные методы, где экстремум функции находится последовательно при движении в направлении возрастания или убывания функции в соответствии с вычисленными на каждом шаге значениями градиентов. В непрямых методах исходная задача заменяется (аппроксимируется) другой задачей, оптимальное решение которой можно найти. Сюда относятся методы квадратичного, сепарабельного и стохастического программирования.

21.1. АЛГОРИТМЫ РЕШЕНИЯ ЗАДАЧ БЕЗ ОГРАНИЧЕНИЙ

В этом разделе представлены два метода решения задач нелинейного программирования без ограничений на переменные: метод прямого поиска и градиентный метод. В первом реализуется прямой поиск оптимальной точки в заданной области, тогда как во втором методе, чтобы найти экстремальную точку, используется градиент целевой функции.

21.1.1. Методы прямого поиска

Методы прямого поиска применяются главным образом для определения экстремумов функций одной переменной. Несмотря на то что такие задачи могут показаться тривиальными, в следующем разделе показано, что методы прямого поиска находят применение и при решении многомерных задач.

Идея методов прямого поиска проста. Сначала определяется интервал неопределенности, который содержит искомую точку оптимума. Затем длина интервала последовательно уменьшается до тех пор, пока не будет найдена точка оптимума. Процедура строится таким образом, что длину интервала, содержащего оптимальное решение, можно сделать сколь угодно малой.

В данном разделе рассматривается метод дихотомического поиска1 и метод золотого сечения. В обоих методах на интервале а<х<Ь ищется максимум функции f(x), имеющей на этом интервале только один максимум. (Такая функция называется одновершинной.) Начальный интервал неопределенности состоит из исходного интервала I0 = (а, Ь).

1 В русскоязычной математической литературе этот метод обычно называется методом деления отрезка пополам. - Прим. ред.

Пусть = (xL, xR) - интервал неопределенности на шаге I (на нулевом шаге xL = а и xR = b). Далее определяем х, и х2 такие, что

х, < х, < х2 <хя.

Следующий интервал неопределенности /, определяется после вычисления значений Дх,) и f(x2). При этом возможны три варианта.

1. Если Дх > f(x2), то точка экстремума х* должна лежать между xL и хг: х, < х < х2. Тогда положим х = х2 и получим новый интервал неопределенности/,= (xL, х2) (рис. 21.1, а).

2. Если f(X]) < f(x2), то хх < х < х . Тогда xL = хг и 7, = (xlt хя) (см. рис. 21.1, б).

3. Если Дх,) = Дх2), то х, < х* < х2. Положим xL = хх и хя = х2, тогда I, = (х х2).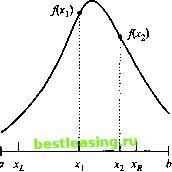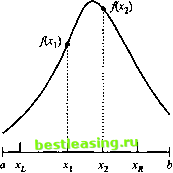

Рис. 21.1. Иллюстрации к прямым методам поиска

Поскольку здесь на каждом шаге гарантировано It < в результате сужается интервал, в котором находится точка максимума функции f(x). Алгоритм заканчивается на некотором шаге k, когда будет выполняться неравенство 1к < Д, где Д - значение заранее заданной точности.

Различие между методами дихотомического поиска и золотого сечения заключается только в способе вычисления точек х, и х2. Формулы для вычисления этих точек, представлены в следующей таблице.

Метод дихотомического поиска

Метод золотого сечения

Xi = (xR + xL- Д)/2

v5-1

Х\ ~ ХК (XR XL>

XZ = (Xr+Xl + A)/2

Xi=XL+-j-(xx-XL)