пуклыми, обеспечивая, таким образом, выпуклость области допустимых решений. Кроме того, считаем, что функции f,(x:) являются выпуклыми в задаче минимизации и вогнутыми в задаче максимизации (см. табл. 20.2 в разделе 20.2.2). При этих условиях можно использовать следующий упрощенный метод аппроксимации.

Рассмотрим задачу минимизации. Пусть функция ft(x) имеет такой вид, как показано на рис. 21.4. Обозначим точки разбиения для функции fx) через xt = ам, k = 0, 1, К,. Пусть xhi - величина изменения переменной xt на интервале (ак , ак), А = 1, 2,К a.ph - тангенс угла наклона линейного сегмента на том же интервале.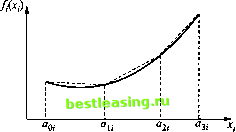

Тогда

Рис. 21.4. Кусочно-линейная аппроксимация выпуклой функции

Здесь предполагается, что 0 < хы < аы - a u, k = 1, 2, Кг

Так как функция /Дх,) выпуклая, то р < р,; <... < pKi,. Это означает, что в задаче

минимизации при р < q большее влияние на значение целевой функции оказывает переменная хр1, чем xql. Следовательно, переменная хр1 всегда будет входить в решение до того, как в него войдет xql При этом значения каждой переменной хк1 должны быть ограничены сверху величиной (ак1 - а4 ).

Выпуклые функции ограничений #/(л->) аппроксимируются аналогичным образом. Пусть pi, - тангенс угла наклона ft-го линейного сегмента, соответствующего функции #/(-*,). Тогда функция аппроксимируется формулой

Следовательно, рассматриваемая задача принимает вид

I ( К:

минимизировать z = 9ихк: + / (а0,)

при ограничениях

0<хк1<ак1- ак и, k=l, 2, tf i = 1, 2,

, g/K)-g/K-u)

Pt; -

Задача максимизации преобразуется аналогично. В этом случае р >p2l >...>pKl,

откуда следует, что при р < q переменная х всегда будет входить в решение раньше хд1 (см. упражнение 21.2.1.7).

Полученную задачу можно решить симплекс-методом, предназначенным для решения задач с ограниченными сверху переменными (раздел 7.3). При этом исчезает необходимость в соблюдении правила ограниченного ввода в базис, поскольку выпуклость (вогнутость) функций гарантирует надлежащий выбор переменных.

Пример 21.2.2

Рассмотрим задачу

максимизировать z = х, - х2

при ограничениях

Зх4+х2<243, х1+2х\<Ъ2, х,>2,1, х2>3,5.

Отдельными (сепарабельными) функциями этой задачи являются

У!(*.) = *.. Ь{хг) = ~хг< j(x1) = 3x14, g\{x2) = x2,

gl{*\) = x\> gl{xi) = 2xl-Эти функции выпуклые, что и требуется в задачах минимизации.

Область допустимых значений переменных хх и х2, как следует из ограничений задачи, определяется неравенствами 0<Xj<3 и 0<х2<4. Разбиваем эти интервалы изменения переменных х, и х2. Пусть А , = 3 и К2 = 4 при а01 = а02 = 0. Значения тангенсов углов наклона, соответствующих отдельным функциям рассматриваемой задачи, приведены в следующих таблицах.

Для i = 1 имеем

Для i = 2 имеем

Теперь задача принимает следующий вид.

Минимизировать z ~ хп + х21 + х31 - х12 - х22 - х32 - х42 при ограничениях

Зхи + 45х21 + 195х31 +х12 +х22 + х32 +х42< 243, хп +х21 +х31 + 2х12 + 6х22 + Юх32 + 14х42 < 32, хп +х21 Ьх31 2,1,

*12 + 22 + 32 + Xi2 S 3,5,

0<xtl < 1, к= 1, 2, 3, 0<xi2< 1,к= 1,2,3,4. С помощью программы TORA получено следующее оптимальное решение:

z = -0,52, хп = х12 = 1, х13 = 0,98, х21 = х22 = х23 = 1, х24 = 0,5. Отсюда получаем решение исходной задачи (х х2) = (2,98, 3,5).

УПРАЖНЕНИЯ 21.2.1

1. Для следующей задачи постройте аппроксимирующую модель в виде задачи частично-целочисленного программирования.

Максимизировать z = е~х + х, + (х2 +1)2

при ограничениях

х,2 + х2 < 3, х х2>0.

2. Решите аппроксимирующую задачу из предыдущего упражнения, используя правило ограниченного ввода в базис. Затем найдите оптимальное решение исходной задачи.

3. Рассмотрите следующую задачу.

Максимизировать z = х,х2х3

при ограничениях

х,2 + х, + х3 < 4, х х2, х3 > 0.

Постройте аппроксимирующую задачу в виде задачи линейного программирования с учетом дальнейшего использования правила ограниченного ввода в базис.