21.2.3. Геометрическое программирование

В геометрическом программировании рассматриваются задачи нелинейного программирования специального вида. Подход геометрического программирования позволяет находить решение исходной задачи с помощью соответствующей двойственной задачи.

Методами геометрического программирования решаются нелинейные задачи, в которых как целевая функция, так и функции ограничений имеют следующий вид:

г = /(Х) =

uj=cjfl*?> У = Ь2,...,Л.

Предполагается, что здесь все с;. > 0, а число N является конечным. Показатели степени atj по знаку не ограничены. Функция /(X) имеет вид полинома, если не учитывать того, что показатели степени atj могут принимать отрицательные значения. По этой причине, а также в связи с тем, что все коэффициенты с; > 0, функция /(X) называется позиномом.

В этом разделе будут рассмотрены задачи геометрического программирования без ограничений. Исследование задач геометрического программирования с ограничениями выходит за рамки настоящей главы. Детальное рассмотрение излагаемых здесь вопросов содержится в книге [2], глава 6.

Рассмотрим задачу минимизации позиномиальной функции /(X). Будем называть эту задачу прямой. Предполагается, что переменные xt принимают строго положительные значения, т.е. область xt < 0 недопустима. Далее будет показано, что требование х Ф 0 является существенным при получении основных результатов.

Первые частные производные функции z в точке минимума должны обращаться в нуль. Следовательно,

Поскольку по предположению все хк > 0, имеем

= 0 = -JXt/., А =1,2,...,я.

Эх x,

к У-1

Пусть z - минимальное значение функции z. Очевидно, что z > 0, так как z - по-зином, и все хк > 0. Обозначим

Из определения следует, что у1 > 0 и X-i-vj = Величина yt характеризует относительный вклад у-го слагаемого V в оптимальное значение целевой функции z. Необходимые условия экстремума теперь можно записать в следующем виде.

I>V,=0. к = 1,2.....я.

Z-Уу = У) > 0 для всех J-

Эти уравнения, именуемые условиями ортогональности и нормировки, определяют единственное решение для yj при условии, что все уравнения независимы и п + 1 = N. Задача усложняется при N > п + 1, так как в этом случае решение для I/. не является единственным. Ниже показано, что и в этом случае существует возможность однозначно определить у. для минимизации функции z.

Пусть yj - элементы единственного решения представленной выше системы

уравнений. Тогда величины г* и х], i = 1, 2,п , определяются следующим образом. Рассмотрим величину

Поскольку Z* = -г , то

П Пс)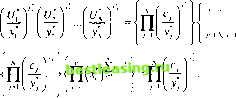

В последнем выражении учтено условие X -iav-vj = Следовательно, значение г можно вычислить, как только будут определены все уг При известных у] я z можно определить U] = у*г* Значения х] находятся как решение системы уравнений

Рассмотренная процедура показывает, что исходная задача минимизации позино-ма z может быть сведена к решению системы линейных уравнений относительно у. При этом значения всех у* определяются из необходимых условий существования

минимума. Можно показать, что эти условия являются также и достаточными. Доказательство этого приводится в книге [2].

Фактически переменные yt определяют двойственные переменные, соответствующие прямой задаче минимизации z. Чтобы установить эту зависимость, запишем целевую функцию прямой задачи в виде

Определим теперь функцию

Поскольку ,у, = 1 и yj > О, в силу неравенства Коши1 имеем w<z.

Функция w с переменными ух, у2, yN определяет задачу, двойственную к исходной. Поскольку w является нижней границей значений z и рассматривается задача минимизации г, то, максимизируя функцию w, мы получим

w = max w = min z = z

У) *:

Это значит, что максимальное значение w (= w ) на множестве допустимых значений г/, совпадает с минимальным значением z (= z ) на множестве допустимых значений xt.

Пример 21.2.4

В этом примере рассматривается задача, где N = п + 1, так что решение, получаемое из условий ортогональности и нормировки, является единственным. (Следующий пример иллюстрирует случай, когда N > п + 1.)

Рассмотрим задачу

минимизировать z = 7х,х; + 3x,xf + 5х~3х,х3 + х,х,х3.

Эту функцию можно записать в виде

z = 7х!х,-х + 3x°xU2 + 5х73х\х\ + х\х\х\,

так что здесь

(с с2, с3, ct) = (7, 3, 5, 1), а а а,3 а14 Г 1 0-3 Г

а,. а а а,.

-1111 0-211

чя3, а а33 а,4/

Условия ортогональности и нормировки приводят к системе уравнений

Эта система имеет единственное решение

.1.1

Следовательно,

= 15,23.

1 Неравенство Коши (неравенство между средним арифметическим и средним геометрическим) устанавливает, что при Zj > 0 выполняется J,%Zy - Г1 -гу Где О > и Xjiy =