при ограничениях

4х, - х2 - 5х3 = 10,

2х, + Зл:2 + 2л:з= 12,

л:, > 0, х2, хъ - свободные переменные.

3.2. ПЕРЕХОД ОТ ГРАФИЧЕСКОГО РЕШЕНИЯ К АЛГЕБРАИЧЕСКОМУ

Идеи, лежащие в основе графического метода решения задач линейного программирования, также являются основой и алгебраического симплекс-метода. На рис. 3.1 показаны параллели между этими двумя методами. В графическом методе пространство решений определяется как пересечение полупространств, порождаемых ограничениями. В симплекс-методе пространство решений задают система из т линейных уравнений и п неотрицательных переменных. Вы должны понимать различие между этими методами, как показано на рис. 3.1 и как будет пояснено на материале этого раздела.

Графический метод

Алгебраический метод

Графическое представление всех ограничений, включая условие неотрицательности

Пространство решений состоит из бесконечного количества допустимых точек

Определяются допустимые угловые точки пространства решений

Кандидатами на оптимальное решение будут конечное число угловых точек

Целевая функция используется для определения оптимальной угловой точки среди всех кандидатов

Задание пространства решений посредством системы из т линейных уравнений с п неотрицательными переменными, т<п

Задача имеет бесконечное количество допустимых решений

Находятся допустимые базисные решения системы уравнений

Кандидатами на оптимальное решение будут конечное число базисных допустимых решений

Целевая функция используется для определения оптимального базисного допустимого решения среди всех кандидатов

Рис. 3.1. Переход от графического решения к алгебраическому

Мы можем увидеть пространство решений графического метода, имеющее бесконечное число точек решений, но как можно сделать подобное заключение на основе алгебраического представления пространства решений? Ответ заключается в том, что в алгебраическом представлении количество уравнений т всегда меньше или равно количеству переменных п.2 Если т = п и система уравнений совместна, то

Если количество уравнений т больше количества переменных п, тогда по крайней мере т - п уравнений должны быть избыточными.

она имеет только одно решение3; если же т< пи система уравнений совместна, то она имеет бесконечное множество решений. Простая иллюстрация в качестве доказательства: для уравнения х = 2 имеем т = п = 1, а его решение, очевидно, единственное. Для уравнения х + у = 1 имеем т - 1 и п = 2, этому уравнению удовлетворяет бесконечное множество решений (любая точка на прямой х + у=1 будет решением).

В алгебраическом представлении кандидаты на оптимальное решение (т.е. те же угловые точки в графическом представлении) определяются из системы линейных уравнений следующим образом. Пусть т < п (это условие выполняется для большинства задач ЛП), тогда полагаем п - т переменных равными нулю и решаем систему из т уравнений относительно оставшихся т переменных; если решение этой системы единственно, то оно соответствует угловой точке пространства решений.

Следующий пример иллюстрирует это положение.

Пример 3.2.1

Рассмотрим следующую задачу ЛП с двумя переменными.

Максимизировать z= 2хх + Зх2

при выполнении условий

2.v,+x,<4, хх + 2х.г < 5, xltx2>0.

На рис. 3.2 показано пространство решений для этой задачи. х2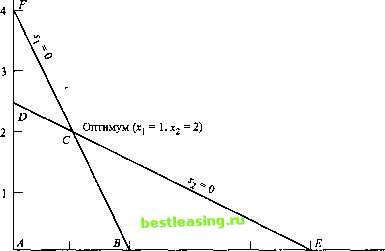

0 1 2 3 4 5

Рис. 3.2. Пространство решений для примера 3.2.1

Это не совсем верно: совместная система уравнений имеет единственное решение тогда, когда она невырождена. - Прим. ред.

После преобразования к стандартной форме имеем следующую задачу ЛП.

Максимизировать z = 2хх + Зхг

при выполнении условий

2дг, + х2 + s, = 4, я, + 2хг + s2 = 5,

*2* 1 2 - *

Здесь имеем систему из т = 2 уравнений для л = 4 переменных. Согласно сформулированному выше правилу угловые точки можно определить алгебраически, присвоив я-т = 4- 2 = 2 переменным нулевых значений и решив затем систему уравнений относительно оставшихся т = 2 переменных. Если, например, положить х1 = 0их2 = 0, тогда решением системы будет s, = 4, s2 = 5. Это решение соответствует точке Л на рис. 3.2 (убедитесь, что решение 5, = 4, s2 = 5 действительно соответствует точке А). Другую угловую точку можно определить, если положить s, = 0 и 52 = 0. В этом случае надо найти решение системы

2хх + х2 = 4,

л-! + 2д-2 = 5.

Решением в данном случае будет jt, = 1 и х, = 2, что соответствует точке С на рис. 3.2.

Вас, вероятно, интересует, как определить, какие п - т переменные положить равными нулю, чтобы получить конкретную угловую точку. Без графического представление пространства решений (что возможно только для задач с двумя и тремя переменными) нельзя сказать, какие п - т нулевые переменные соответствуют той или иной угловой точке. Однако это не мешает перечислить все угловые точки пространства решений. Для этого надо просто рассмотреть все комбинации п - т переменных, приравнять их к нулю и затем найти решение полученной системы уравнений. Оптимальное решение, которое доставляет наилучшее значение целевой функции, будет среди допустимых угловых точек.

В нашем примере мы имеем = Tj= Угловых точек. Но, глядя на рис. 3.2,

можно насчитать только 4 угловые точки -А, В, С nD. Где спрятались еще две точки? В действительности точки Е и F также являются угловыми точками, но это недопустимые угловые точки, поскольку они не удовлетворяют всем ограничениям задачи. Такие недопустимые угловые точки не рассматриваются как кандидаты на оптимальное решение.

Для полного перехода к алгебраическому методу решения задач ЛП необходимо как-то назвать угловые точки разного типа на алгебраическом языке. На этом языке п - т переменные, которые полагаются равными нулю, называются небазисными переменными. Если оставшиеся т переменные имеют единственное решение, то в этом случае они называются базисными переменными, а совокупность значений, которые они получают в результате решения системы уравнений, составляют базисное решение (см. рис. 3.1). Если при этом все переменные принимают неотрицательные значения, то такое базисное решение является допустимым. В противном случае - недопустимым.4

i В русскоязычной математической литературе также применяются термины план , опорный план и оптимальный опорный план как эквиваленты для терминов базисное решение , допустимое базисное решение и оптимальное базисное решение . - Прим. ред.