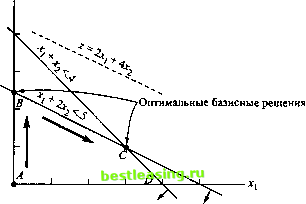Рис. 3.11. Альтернативные оптимумы в примере 3.5.2

На первой итерации получаем оптимальное решение х, = 0, х2 = 5/2 и z = 10, которое соответствует точке В на рис. 3.11. Как узнать из симплекс-таблицы, что существует альтернативное оптимальное решение? Посмотрите на коэффициенты небазисных переменных в г-строке первой итерации. Коэффициент небазисной переменной д-, равен нулю, это означает, что данную переменную можно ввести в базис без изменения значения целевой функции, но значение самой переменной д-, изменится. Введение переменной хх в базисное решение выполнено на второй итерации, при этом из базиса исключена переменная xt. Получено новое решение х, = 3, х2 = 1, z = 10, которое соответствует точке Сна рис. 3.11.

Симплекс-метод может определить только две угловые точки В и С. Математически мы можем найти все точки (лгрдг) отрезка ВС как взвешенное среднее (с неотрицательными весами) точек В и С. Если 0 < ос < 1 и

В: х, = 0, х, = 5/2,

С. дг, = 3, х2 = 1,

координаты любой точки отрезка ВС можно записать следующим образом:

х\ = а х 0 + (1 - а) х 3 = 3 - За,

л\ = ах - + (1 - а) х 1 = 1 + - а. 2 2

При а = 0 (х\,хг) = (3, 1), что соответствует точке С. При а=1 получаем <х[,х2) = (0, 5/2) - это точка В. Если значение а лежит строго между 0 и 1, получаем внутренние точки отрезка ВС.

На практике альтернативные оптимальные решения весьма полезны, поскольку позволяют сделать выбор среди множества решений без ухудшения значения целевой функции. Например, в рассмотренной выше задаче переменная л:2 принимает нулевое значение в точке В, тогда как в других альтернативных оптимальных решениях ее значение положительно. Если интерпретировать задачу как задачу организации производства двух видов товара (которые соответствуют переменным д;, и д;2), то с учетом конкуренции на рынке более рационально производить оба вида товара, а не один. В этом случае решение, соответствующее точке С, предпочтительнее.

УПРАЖНЕНИЯ 3.5.2

1. Для следующей задачи ЛП найдите не менее трех альтернативных оптимальных базисных решений. Запишите также общее выражение для всех небазисных альтернативных оптимальных решений, частными случаями которых будут найденные ранее решения.

Максимизировать г = х, + 2х2 + Зх3

при выполнении условий

x,+2x2-l-3x3<10, х, + х2 < 5,

х х2, х3>0.

2. Покажите с помощью программы TORA, что следующая задача ЛП имеет альтернативные оптимальные решения и все они небазисные. Для этой задачи представьте на плоскости пространство решений и прямую, соответствующую целевой функции.

Максимизировать г = 2х, - х2 + Зх3

при выполнении условий

х, - х2 + 5х3< 10, 2х, - х2 + Зх3 < 40, *i> х2, х3>0.

3. Покажите с помощью программы TORA, что в следующей задаче ЛП оптимальное решение вырождено, и все существующие альтернативные решения являются небазисными.

Максимизировать z = Зх, + х2 при выполнении условий

х, + 2х2<5, х1 + х2-х3<2, 7х, + Зх2 - 5х3 < 20, х х2, х3>0.

3.5.3. Неограниченные решения

В некоторых задачах ЛП значения переменных могут неограниченно возрастать без нарушения ограничений. Это говорит о том, что пространство допустимых решений не ограничено по крайней мере по одному направлению. В результате этого целевая функция может возрастать (задача максимизации) или убывать (задача минимизации) неограниченно.

Неограниченность решения задачи свидетельствует только об одном: модель разработана не достаточно корректно. Типичные ошибки, приводящие к построению таких моделей, заключаются в том, что не учитываются ограничения, не являющиеся избыточными, и не точно оцениваются параметры (коэффициенты) ограничений.

В следующем примере показано, как на основе данных, приведенных в симплекс-таблице, можно определить, когда не ограничено пространство решений и значения целевой функции.

Пример 3.5.3. Неограниченная целевая функция

Рассмотрим задачу

максимизировать z = 2х, + х2

при выполнении условий

хг-х2<10, 2х, < 40, xv х2 > 0.

Симплекс-таблица начальной итерации этой задачи имеет следующий вид.

Из этой таблицы видно, что в качестве вводимой переменной можно взять как х так и х2. Поскольку переменная х} имеет максимальный (по абсолютной величине) отрицательный коэффициент в z-строке, именно ее следует ввести в базисное решение. Однако заметим, что во всех ограничениях коэффициенты, стоящие перед переменной х2, отрицательны или равны нулю. Это означает, что значение переменной х2 может возрастать до бесконечности, и при этом не нарушается ни одно ограничение. Поскольку увеличение на 1 значения переменной х2 приводит к увеличению на 1 значения целевой функции, следовательно, неограниченное увеличение значения переменной хг ведет к неограниченному увеличению значения целевой функции. Эта ситуация проиллюстрирована на рис. 3.12. На этом рисунке видно, что пространство допустимых решений не ограничено в направлении оси х2, и значение целевой функции может быть каким угодно большим.

Неограниченное пространство решений

2x40

Неограниченное значение целевой функции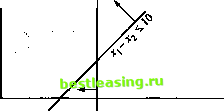

Рис. 3.12. Неограниченность решения в примере 3.5.3