Следующая таблица получена с помощью известных операций над строками, применяемых в прямом симплекс-методе.

На рис. 4.2 показана последовательность шагов двойственного симплекс-метода при решении задачи из примера 4.4.1. Алгоритм начинается в крайней точке А (которой соответствует недопустимое, но лучше, чем оптимальное решение), затем он переходит к точке В (которой также соответствует недопустимое, но лучше, чем оптимальное решение) и заканчивается в точке С, уже принадлежащей области допустимых решений.

Программа TORA позволяет выполнять двойственный симплекс-метод в пошаговом режиме. Для этого -в меню SOLVE/MODIFY выберите команду SolveAlgeraic Iterations1 Dual Simplex (Решить1АлгебраическиИтерацииОДвойственный симплекс-метод). Помните, что сначала надо ограничения в виде равенств преобразовать в неравенства. Неравенства типа > преобразовывать в противоположные неравенства не нужно, поскольку TORA автоматически выполнит преобразование задачи к виду, необходимому для применения двойственного симплекс-метода. Если задача не удовлетворяет начальным требованиям для применения двойственного симплекс-метода, то на экране появится соответствующее сообщение. Как и в обычном симплекс-методе, здесь в пошаговом режиме TORA позволяет вручную указывать вводимые и исключаемые переменные.

УПРАЖНЕНИЯ 4.4.1

1. На рис. 4.3 показано пространство решений, соответствующее задаче минимизации целевой функции z = 2х, + х2. Предполагается, что поиск решения выполняется двойственным симплекс-методом; оптимальное решение соответствует точке F - (0,5, 1,5).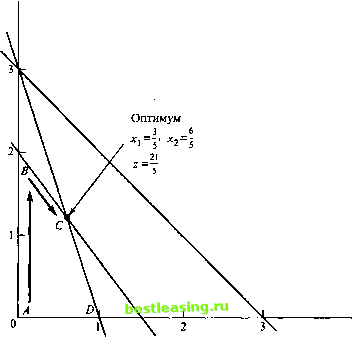

Рис. 4.2. Итерации двойственного симплекс-метода из примера 4.4.1 х2

Рис. 4.3. Пространство решений для задачи упражнения 1

а) Если начальное базисное (недопустимое) решение соответствует точке G, будет ли алгоритм двойственного симплекс-метода проходить через точки G, Е, F7 Обоснуйте это.

Ь) Если начальное базисное (недопустимое) решение соответствует точке L, определите на рис. 4.3 возможную последовательность точек, через которые будет проходить алгоритм двойственного симплекс-метода для достижения оптимального решения в точке F.

2. Решите следующие задачи двойственным симплекс-методом с помощью программы TORA и определите на графически представленном пространстве решений этих задач последовательность точек прохождения алгоритма двойственного симплекс-метода для достижения оптимального решения.

a) Минимизировать z = 2хл 4- 3jc2 при ограничениях

2хг + 2х2 < 30, х1 + 2х2>10, х х2>0.

b) Минимизировать z = 5х1 + 6х2 при ограничениях

х1+ х2> 2, 4х1 + х2 > 4, xv х2>0.

c) Минимизировать z - 4дс, + 2х2 при ограничениях

х1 + х2 = 1, 3xx2, хг, jc2>0.

d) Минимизировать z = 2лс, + Зх2 при ограничениях

2х, + л:2 > 3, xt+x2 = 2, xv х2 > 0.

3. Двойственный симплекс-метод с искусственными ограничениями. Дана следующая задача ЛП.

Максимизировать z = 2xt - х2 + х3

при ограничениях

2хг + Зх2-5х3>4, -л:, + 9х2- х3> 3, 4х, + 6х2 + Зх3 < 8, х х2, х3>0.

Начальное базисное решение содержит дополнительные переменные х4, хь их6 и является недопустимым, поскольку х4 = -4 и хб = -3. Но непосредственное применение двойственного симплекс-метода невозможно, так как переменные х1 и х3 не удовлетворяют условию оптимальности для задачи максимизации. Покажите, что введение искусственного ограничения х1 + х3<М (где М- достаточно большое положительное число и такое, что данное неравенство не сужает область допустимых решений исходной задачи) и последующее использование