ГЛАВА 5

ТРАНСПОРТНЫЕ МОДЕЛИ

Транспортные модели (задачи) - специальный класс задач линейного программирования. Эти модели часто описывают перемещение (перевозку) какого-либо товара из пункта отправления (исходный пункт, например место производства) в пункт назначения (склад, магазин, грузохранилище). Назначение транспортной задачи - определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов в пунктах назначения (спрос). В транспортной модели предполагается, что стоимость перевозки по какому-либо маршруту прямо пропорциональна объему груза, перевозимого по этому маршруту. В общем случае транспортную модель можно применять для описания ситуаций, связанных с управлением запасами, управлением движением капиталов, составлением расписаний, назначением персонала и др.

Хотя транспортная задача может быть решена как обычная задача линейного программирования, ее специальная структура позволяет разработать алгоритм с упрощенными вычислениями, основанный на симплексных отношениях двойственности. В данной главе будет показан этот алгоритм и его тесная связь . с симплекс-методом.

5.1. ОПРЕДЕЛЕНИЕ ТРАНСПОРТНОЙ МОДЕЛИ

На рис. 5.1 показано общее представление транспортной задачи в виде сети с т пунктами отправления и п пунктами назначения, которые показаны в виде узлов сети. Дуги, соединяющие узлы сети, соответствуют маршрутам, связывающим пункты отправления и назначения. С дугой (i, j), соединяющей пункт отправления i с пунктом назначения j, соотносятся два вида данных: стоимость с, перевозки единицы груза из пункта i в пункт j и количество перевозимого груза х . Объем грузов в пункте отправления / равен а а объем грузов в пункте назначения j - b . Задача состоит в определении неизвестных величин х , минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям, налагаемым на объемы грузов в пунктах отправления (предложения) и пунктах назначения (спрос).

Пункты отправления Пункты назначения

Объемы предложений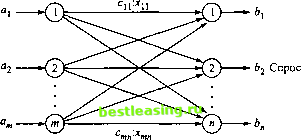

Рис. 5.1. Представление транспортной задачи

Пример 5.1.1

Автомобильная компания MG Auto имеет три завода в Лос-Анджелесе, Детройте и Новом Орлеане и два распределительных центра в Денвере и Майами. Объемы производства заводов компании в следующем квартале составят соответственно 1000, 1500 и 1200 автомобилей. Ежеквартальная потребность распределительных центров составляет 2300 и 1400 автомобилей. Расстояния (в милях) между заводами и распределительными центрами приведены в табл. 5.1.

Таблица 5.1

Транспортная компания оценивает свои услуги в 8 центов за перевозку одного автомобиля на расстояние в одну милю. В результате получаем следующую стоимость перевозок (с округлением до доллара) по каждому маршруту.

Таблица 5.2

Основываясь на данных из табл. 5.2, формулируем следующую задачу линейного программирования.

Минимизировать z = 80jc + 215.v12 + 100.v21 +108x22 + 102jt31 + 68x32 при ограничениях

xu + jc12 = 1000 (Лос-Анджелес),

jc21 + jc22 = 1500 (Детройт),

*3i + хз2 = 1200 (Новый Орлеан),

хи + х21 + х31 = 2300 (Денвер),

х12 + х22 + х32 = 1400 (Майами),

xtj>0, /=1,2,3,7 = 1,2.

Эти ограничения выражены в виде равенств, поскольку общий объем произведенных автомобилей (1000 + 1500 + 1200 = 3700) равен суммарному спросу распределительных центров(2300 + 1400 = 3700).

Данную задачу ЛП можно решить симплекс-методом. Но специфическая структура ограничений позволяет решить эту задачу более простым способом с помощью так называемой транспортной таблицы (табл. 5.3).

Таблица 5.3

Денвер Майами Объем производства

Оптимальное решение (полученное с помощью программы TORA ) показано на рис. 5.2. Оно предполагает перевозку 1000 автомобилей из Лос-Анджелеса в Денвер, 1300 автомобилей- из Детройта в Денвер, 200 автомобилей- из Детройта в Майами и 1200 - из Нового Орлеана в Майами. Минимальная стоимость перевозок составляет 313 200 долл.

1000-

150О

120О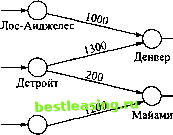

2300

1400

Новый Орлеан

Рис. 5.2. Схема оптимальных перевозок

Чтобы получить в программе TORA решение транспортной задачи, в меню Main Menu выберите команду Transportation Model (Транспортная модель). Затем в меню SOLVE/MODIFY выберите команду Solved Final solution. Более подробно решение транспортных задач в программе TORA описано в разделе 5.3.3.