УПРАЖНЕНИЯ 2.1

1. В модели для компании Reddy Mikks сформулируйте новые ограничения, исходя из следующих условий.

a) Ежедневный объем производства краски для внутренних работ должен не менее чем на одну тонну превышать ежедневный объем производства краски для наружных работ.

b) Ежедневное потребление сырья М2 должно быть не менее 3 т и не более 6 т.

c) Ежедневный объем производства краски для внутренних работ не может быть меньше ежедневного объема производства краски для наружных работ.

d) Минимальный ежедневный общий объем производства краски обоих типов составляет 3 т.

e) Отношение ежедневного объема производства краски для внутренних работ к общему объему производства краски обоих типов не должно превышать 0,5.

2. Для компании Reddy Mikks найдите оптимальное допустимое решение модели среди следующих решений.

3. Для допустимого решения л:, = 2, х2 = 2 в модели компании Reddy Mikks определите:

a) объем используемого сырья Ml;

b) объем используемого сырья М2.

4. Предположим, что компания Reddy Mikks продает свою краску для наружных работ оптовому покупателю со скидкой, зависящей от объема поставок. В результате доход на тонну продукции составляет 5000 долл., если оптовик покупает не более 2 т краски в день, и 4500 долл. - в противном случае. Можно ли для этой ситуации построить модель линейного программирования?

2.2. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Графический способ решения задачи ЛП состоит из двух этапов.

1. Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели.

2. Поиск оптимального решения среди всех точек пространства допустимых решений.

Далее графический способ решения описан в двух вариантах: для максимизации и минимизации целевой функции.

2.2. Графическое решение задачи линейного программирования 2.2.1. Нахождение максимума целевой функции

Пример 2.2.1

Мы используем модель, построенную для компании Reddy Mikks в разделе 2.1, чтобы показать два этапа графического решения задачи ЛП.

Этап 1. Построение пространства допустимых решений.

Сначала проведем оси: на горизонтальной будут указываться значения переменной xlt а на вертикальной - хг (рис. 2.1). Далее рассмотрим условие неотрицательности переменных: л, > 0 и х2 > 0. Эти два ограничения показывают, что пространство допустимых решений будет лежать в первом квадранте (т.е. выше оси х1 и правее оси х2).

Чтобы учесть оставшиеся ограничения, проще всего заменить неравенства на равенства (получив уравнения прямых), а затем на плоскости провести эти прямые. Например, неравенство 6х1 + 4х2 < 24 заменяется уравнением прямой 6х, + 4х2 = 24. Чтобы провести эту линию, надо найти две различные точки, лежащие на этой прямой. Если х, = 0, то х2 = 24/4 = 6. Аналогично для х2 = 0 находим х1 = 24/6 = 4. Итак, наша прямая проходит через две точки (0, 6) и (4, 0). Эта прямая обозначена на рис. 2.1 как линия (1).

Теперь рассмотрим, как графически интерпретируются неравенства. Каждое неравенство делит плоскость (xv х2) на два полупространства, которые располагаются по обе стороны прямой, которая, как показано выше, соответствует данному неравенству. Точки плоскости, расположенные по одну сторону прямой, удовлетворяют неравенству (допустимое полупространство), а точки, лежащие по другую сторону, - нет. Тестовой точкой, проверяющей, точки какого полупространства удовлетворяют

Ограничения: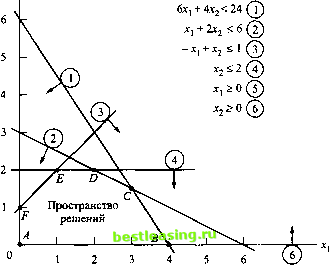

Рис. 2.1. Пространство допустимых решений модели

неравенству, а какого - нет, может служить точка (0, 0). Например, эта точка удовлетворяет первому неравенству 6xt + 4х2 < 24 (здесь 6х0+4х0=0< 24). Это означает, что точки полупространства, содержащего начальную точку (0, 0), удовлетворяют этому неравенству. На рис. 2.1 допустимые полупространства показаны стрелочками.

Если точка (0, 0) не удовлетворяет неравенству, допустимым полупространством будет то, которое не содержит эту точку. Если же прямая проходит через эту точку, следует в качестве тестовой взять какую-либо другую точку.

Этап 2. Поиск оптимального решения.

Точки пространства допустимых решений, показанного на рис. 2.1, удовлетворяют одновременно всем ограничениям. Это пространство ограничено отрезками прямых, которые соединяются в угловых точках Л, В, С, D, Е и F. Любая точка, расположенная внутри или на границе области, ограниченной ломаной ABCDEF, является допустимым решением, т.е. удовлетворяет всем ограничениям. Поскольку пространство допустимых решений содержит бесконечное число точек, необходима некая процедура поиска оптимального решения.

Для того чтобы найти оптимальное решение, необходимо определить направление возрастания целевой функции z = 5х1 + 4х2 (напомним, что функцию z следует максимизировать). Мы можем приравнять z к нескольким возрастающим значениям, например 10 и 15. Эти значения, подставленные вместо z в выражение целевой функции, порождают уравнения прямых; для значений 10 и 15 получаем уравнения прямых 5х, + 4х2 = 10 и 5xj + 4х2 = 15. На рис. 2.2 эти прямые показаны штриховыми линиями, а направление возрастания целевой функции - жирной стрелкой.2 Целевая функция может возрастать до тех пор, пока прямые, соответствующие возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.

На рис. 2.2 видно, что оптимальное решение соответствует точке С. Эта точка является местом пересечения прямых (1) и (2), поэтому ее координаты хх и х2 находятся как решение системы уравнений, задающих эти прямые:

6х, + 4х2 = 24,

Xl + 2x2 = 6.

Решением этой системы будет xt = 3 и х2= 1,5, при этом значение целевой функции равно z = 5x3 + 4x1,5 = 21. Полученное решение означает, что для компании Reddy Mikks оптимальным выбором будет ежедневное производство 3 т краски для наружных работ и 1,5 т - для внутренних работ с ежедневным доходом в 21 000 долл.

Не случайно, что оптимальное решение расположено в угловой точке пространства допустимых решений, где пересекаются две прямые. Если мы изменим наклон функции z (путем изменения ее коэффициентов), то обнаружим, что в любом случае решение достигается в одной из угловых точек (или одновременно в нескольких угловых точках). В этом и состоит основная идея построения общего симплексного алгоритма, который будет рассмотрен в главе 3.

Направление изменения целевой функции легко определить из вида целевой функции: коэффициенты при переменных х1и хг - это координаты нормали к прямой, определяемой целевой функцией. В данном случае целевая функция будет изменяться в направлении вектора (5; 4). - Прим. ред.