поставлены четыре новых станка, местоположение которых обозначено кружочками с буквами а, Ь, с и d. Необходимо так разместить новые станки, чтобы минимизировать суммарные перемещения обрабатываемых деталей между новыми и старыми станками. В табл. 5.43 показана интенсивность перемещения деталей между новыми и старыми станками. Детали перемещаются по сторонам прямоугольника, противоположными вершинами которого будут старый и новый станки. Например, расстояние (в метрах) между станком 1 и станком, расположенным в позиции Ь, равно 30 + 20 = 50 м.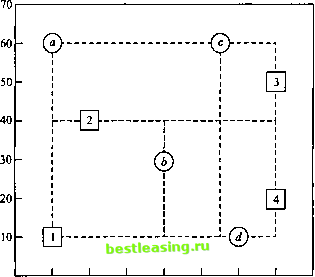

О 10 20 30 40 50 60 70 80 Рис. 5.8. Расположение станков в задаче упражнения 6

Таблица 5.43

Старые станки

Новые станки 2 3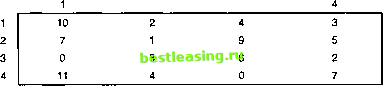

5.4.2. Интерпретация венгерского метода как симплекс-метода

Задачу о назначении п работников на п видов работ можно представить в виде задачи линейного программирования следующим образом. Обозначим через с(/ стоимость назначения работника i на работу у и определим

1, если работник / назначен на работу у, 0, в противном случае.

Получаем следующую задачу ЛП.

Минимизировать z = dcjjxij

при выполнении условий

2>, = 1, i = l, 2,..., и.

5> =1, У = 1,2,..., и, л:. = 0 или 1.

Оптимальное решение данной задачи ЛП останется неизменным, если ко всем элементам какой-либо строки или столбца матрицы стоимостей (с,.) прибавить константу или вычесть ее из этих элементов. Для доказательства этого обозначим через pt и <7у константы, вычитаемые из элементов строки i и столбца у соответственно. Таким образом, стоимость с изменится и будет равна

Теперь покажем, что при коэффициентах целевой функции с получим те же оптимальные значения переменных jc ., что и при коэффициентах сц.

ХЕ<с - а - я,)**=ХХсл - X р. (х** ] ~ X?; f Х-1= = XXca - X p> 0) X<?;( 0=ХХсл константа-

Поскольку новая целевая функция отличается от исходной только на константу, оптимальные значения переменных х должны быть одинаковы в обоих случаях. Таким образом показано, что этапы 1 и 2 венгерского метода, где р. вычитаются из элементов строки г, a. q - из элементов столбца у матрицы стоимостей, приводят к эквивалентной задаче о назначениях. Поэтому, если нулевые элементы в матрице стоимостей, созданные на этапе 1 и 2 венгерского метода, позволяют найти допустимое решение, то оно должно быть оптимальным, поскольку стоимости в измененной матрице стоимостей не могут быть меньше нуля.

Если созданные нулевые элементы не могут привести к допустимому решению (как в примере 5.4.2), необходимо выполнить описанный выше этап 2.1. Эта процедура опять основывается на симплекс-методе, и ее корректность можно обосновать, исходя из теории двойственности (глава 4) и теоремы о дополняющей нежесткости (глава 7). Пока мы не будем углубляться в это.

То, что сумма Хр, +Xjj равна оптимальному значению целевой функции,

вытекает из того, что данная сумма представляет собой целевую функцию двойственной задачи. Это видно из представленного в разделе 5.3.4 выражения для целевой функции задачи, двойственной транспортной задаче. (Подробности см. в [1].)

5.5. ТРАНСПОРТНАЯ МОДЕЛЬ С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ

Транспортная модель с промежуточными пунктами соответствует реальной ситуации, когда между исходными и конечными пунктами перевозок имеются промежуточные пункты для временного хранения грузов (транзитные пункты). Эта

модель более общая, чем обычная транспортная, где перевозки осуществляются непосредственно между пунктами отправления и назначения.

В этом разделе показано, как транспортную модель с промежуточными пунктами можно преобразовать (и решить) в обычную транспортную с помощью введения буфера.

Пример 5.5.1

Два автомобильных завода Р1 и Р2 связаны с тремя дилерами Dl, D2 и D3, имеющими два транзитных (перевалочных) центра Т1 и Т2, как показано на рис. 5.9. Заводы Р1 и Р2 производят 1000 и 1200 автомобилей. Заказы дилеров составляют соответственно 800, 900 и 500 автомобилей. Стоимость перевозок одного автомобиля (в сотнях долларов) показана на рис. 5.9 возле соответствующих дуг.

1000-

120О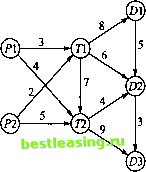

Рис. 5.9. Транспортная модель с промежуточными пунктами

В данной модели перевозки транзитом могут осуществляться через любые пункты (в соответствии с направлением дуг на схеме), даже через некоторые пункты назначения. Поэтому пункты, которым соответствуют как входящие, так и выходящие дуги на схеме рис. 5.9, назовем транзитными (пункты 71, 72, D1 и D2). Оставшиеся будут либо истинными пунктами отправления (пункты Р1 и Р2), либо истинными пунктами назначения (в данной схеме такой пункт только один - D3). Эту модель можно преобразовать в обычную транспортную модель с шестью пунктами отправления (PI, Р2, 71, 72, D1 и D2) и пятью пунктами назначения (71, 72, Dl, D2 и D3). Объемы спроса и предложения, соответствующие этим пунктам отправления и назначения, вычисляются следующим образом.

Объем предложения истинного пункта отправления = объем исходного предложения.

Объем предложения транзитного пункта - объем исходного предложения + объем буфера.

Объем спроса истинного пункта назначения = объем исходного спроса.

Объем спроса транзитного пункта = объем исходного спроса + + объем буфера.

Объем буфера должен быть таким, чтобы вместить объем всего предложения (или спроса). Обозначим через В объем буфера. Тогда