5. Предположим, что в предыдущей задаче (рис. 6.8) все добывающие платформы разбиты на две группы в зависимости от давления газа в скважинах: к группе с высоким давлением газа относятся платформы 2, 3, 4 и 6, с низким давлением - 5, 7, 8 и 9. Из-за разницы в давлении газопроводы от платформ разных групп нельзя соединять между собой. В то же время газопроводы от этих групп могут подсоединяться к приемному пункту через платформу 1. Определите минимальную сеть трубопроводов для данной ситуации.

6. Компания производит 15 типов изделий на 10 станках. Она планирует сгруппировать станки так, чтобы минимизировать несходство операций, выполняемых на каждой группе станков. Мерой несходства между станками i и у служит величина d,., вычисляемая по формуле

где пц - количество изделий, обрабатываемых как на станке i, так и на станке у, тц - количество изделий, обрабатываемых только на станке i или только на станке у.

В следующей таблице показано, изделия каких типов на каких станках обрабатываются.

a) Сформулируйте данную задачу как сетевую.

b) Покажите, что разбить множество станков на группы можно, решив задачу нахождения минимального остовного дерева.

c) Решите данную задачу для разбиения станков на две и три группы.

6.3. ЗАДАЧА ПОИСКА КРАТЧАЙШЕГО ПУТИ

Данная задача состоит в определении в транспортной сети кратчайшего пути между заданными исходным пунктом и пунктом назначения. Такую модель можно использовать для описания разнообразных ситуаций, как показано в следующем разделе.

Пример 6.3.1. Замена оборудования

Компания по прокату автомобилей разрабатывает план по обновлению парка своих машин на следующие пять лет (2001-2005 гг.). Каждый автомобиль должен проработать не менее одного и не более трех лет. В следующей таблице приведена стоимость замены автомобиля в зависимости от года покупки и срока эксплуатации.

Задачу можно сформулировать как сетевую с пятью узлами с номерами от 1 до 5, соответствующими годам 2001-2005. Из узла 1 (2001 год) дуги идут только к узлам 2, 3 и 4, поскольку автомобиль может эксплуатироваться не менее одного и не более трех лет. Дуги из других узлов интерпретируются аналогично. Стоимости дуг равны стоимостям замены автомобилей. Решение задачи эквивалентно нахождению кратчайшего пути между узлами 1 и 5.

На рис. 6.9 показана построенная сеть. С помощью программы TORA находим кратчайший путь 1->3->5 (показан на рис. 6.9 жирными линиями). Это решение означает, что автомобили, приобретенные в 2001 году (узел 1), будут эксплуатироваться 2 года, до 2003 года (узел 3), затем они будут заменены новыми, которые будут эксплуатироваться до конца 2005 года. Общая стоимость замены составит 5400 + 7100= 12 500 долл.

9800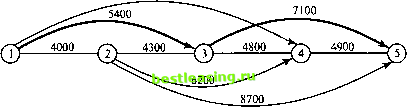

Рис. 6.9. Задача замены оборудования как задача поиска кратчайшего пути

6.3.1. Практические примеры задачи поиска кратчайшего пути

Пример 6.3.2. Самый надежный маршрут

М-р Разумник ежедневно ездит на работу на автомобиле. Закончив в свое время полный курс по теории исследования операций, он легко определил самый короткий путь от дома до работы. К сожалению, данный маршрут усиленно патрулируется нарядами полиции, и автомобиль Разумника часто останавливают за превышение скорости (как ему кажется, не обоснованно). Таким образом, самый короткий путь оказался не самым быстрым. Поэтому м-р Разумник планирует разработать новый маршрут, на котором он имел бы самую высокую вероятность не быть остановленным полицией. Схема сети дорог, по которой м-р Разумник может добраться от дома до работы, показана на рис. 6.10. На этой же схеме приведены вероятности не быть остановленным для каждого сегмента сети дорог. Вероятность не быть остановленным на всем пути следования автомобиля Разумника равна произведению вероятностей не быть остановленным на каждом сегменте выбранного пути. Например, вероятность не быть остановленным на маршруте 1- 3- 5- 7 равна 0,9 х 0,3 х 0,25 = 0,0675. Таким образом, м-ру Разумнику необходимо решить задачу выбора маршрута, который максимизировал бы вероятность не быть остановленным.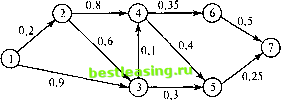

Рис. 6.10. Сетевая модель

Эту задачу можно сформулировать как задачу нахождения кратчайшего пути, если вместо вероятностей использовать логарифмы вероятностей. Тогда произведение вероятностей преобразуется в сумму логарифмов вероятностей: если plk=p1* р2х ... хрк - вероятность не быть остановленным на маршруте 1->2->к, тогда

log plk = log р, + log р2 + ... + log рк.

С точки зрения математики задача максимизации вероятности р1к эквивалентна задаче максимизации величины \ogplk. Поскольку \ogpn<0, задача максимизации величины \ogplk эквивалентна задаче минимизации -logpu. Заменив на рис. 6.10 вероятности рк на величины -\ogpk, получаем сеть (рис. 6.11), к которой можно применить алгоритм определения кратчайшего пути.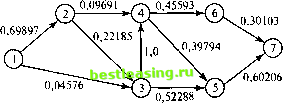

Рис. 6.11. Сетевая модель для задачи поиска кратчайшего пути