С помощью программы TORA находим кратчайший путь для полученной сети: 1- 3- 5- 7 с соответствующей длиной пути 1,1707 (=-logp17). Таким образом, максимальная вероятность не быть остановленным равнар17 = 0,0675.

Пример 6.3.3. Головоломка о трех бидонах

Восьмилитровый бидон заполнен некой жидкостью, а два бидона емкостью 5 и 3 литра пусты. Необходимо разделить 8 литров жидкости на две равные части, используя только три имеющихся бидона. Какое минимальное количество переливаний из бидона в бидон надо сделать, чтобы достичь желаемого результата?

Вы, вероятно, уже нашли решение этой головоломки. Вместе с тем ее можно решить как задачу о нахождении кратчайшего пути.

В этой сетевой модели каждый узел будет соответствовать объемам жидкости в 8-, 5- и 3-литровом бидонах. Начальным узлом будет (8, 0, 0), а конечным - (4, 4, 0). Новый узел получается из текущего при однократном переливании жидкости из одного бидона в другой.

На рис. 6.12 показаны различные маршруты, ведущие от начального узла (8, 0, 0) к конечному (4, 4, 0). Таким образом, наша головоломка сведена к задаче определения кратчайшего пути между узлами (8, 0, 0) и (4, 4, 0).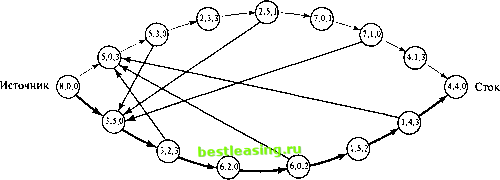

Рис. 6.12. Головоломка о трех бидонах как задача вычисления кратчайшего пути

Оптимальное решение, показанное в нижней части рис. 6.12, требует семи переливаний из бидона в бидон.

УПРАЖНЕНИЯ 6.3.1

1. Создайте заново модель замены оборудования из примера 6.3.1, предполагая, что автомобиль до замены должен эксплуатироваться не менее 2-х и не более 4-х лет. Стоимость замены автомобилей в 2001-2005 годах приведена в следующей таблице.

2. На рис. 6.13 показана коммуникационная сеть между двумя приемно-передающими станциями 1 и 7. Возле каждой дуги этой сети указаны вероятности передачи сообщений без потерь по этим дугам. Необходимо найти маршрут от станции 1 к станции 7 с максимальной вероятностью успешной передачи сообщений. Сформулируйте эту задачу как поиск кратчайшего пути и решите ее с помощью программы TORA.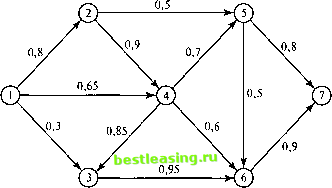

Рис. 6.13. Сеть для задачи из упражнения 2

3. Тостер старой конструкции имеет две подпружиненные дверцы на петлях, размещенные с обеих сторон тостера. Ломтик хлеба помещается в тостер с одной стороны и дверца закрывается, затем другой ломтик хлеба загружается в тостер с противоположной стороны. После того как одна сторона ломтика хлеба подрумянится, он переворачивается. Задача заключается в определении последовательности операций (помещение ломтика хлеба, поджаривание одной стороны, переворачивание ломтика в тостере и извлечение готового хлеба из тостера), необходимых для поджаривания трех ломтиков хлеба за минимально возможное время. Сформулируйте эту задачу как определение кратчайшего пути, используя следующие данные о времени вы-

полнения различных операций.

Операция Время (секунды) Помещение ломтика хлеба в тостер 3

Поджаривание одной стороны ломтика 30

Переворачивание ломтика в тостере 1

Извлечение ломтика из тостера 3

4. Планирование производства. Компания продает некую продукцию, спрос на которую в следующие 4 месяца составит 100, 140, 210 и 180 единиц соответственно. Компания может удовлетворить любой помесячный спрос на продукцию и даже спрос на два и более месяцев вперед. В последнем случае необходимо платить 1,20 долл. за хранение единицы избыточно произведенной продукции в течение месяца. Покупная цена единицы продукции в следующие 4 месяца будет равна 15, 12, 10 и 14 долл. соответственно. Стоимость переналадки оборудования для выполнения заказа составляет 200 долл. Компания хочет разработать такой производственный план, чтобы минимизировать расходы на выполнение заказов, покупку продукции и ее хранение. Сформулируйте задачу как поиск кратчайшего пути и найдите ее оптимальное решение с помощью программы TORA.

5. Задача о рюкзаке. Путешественник, собираясь в путь, пытается поместить в свой рюкзак (объемом 5 кубических футов) наиболее необходимые в путешествии вещи. Есть три вещи, объемом соответственно 2, 3 и 4 кубических фута, необходимость в которых оценивается (по 100-балльной шкале) в 30, 50 и 70 баллов. Сформулируйте эту задачу как сетевую, где необходимо определить самый длинный путь, и найдите ее оптимальное решение. {Совет. Узел в этой сети можно определить как пару [i, и], где i - номер выбираемой вещи, a v - свободный объем рюкзака, оставшийся после выбора t-й вещи.)

6.3.2. Алгоритм определения кратчайшего пути

В этом разделе представлены два алгоритма для решения задачи поиска кратчайшего пути как в сетях, имеющих циклы, так и в сетях, не имеющих циклов.

1. Алгоритм Дейкстры.

2. Алгоритм Флойда.

Алгоритм Дейкстры разработан для поиска кратчайшего пути между заданным исходным узлом и любым другим узлом сети. Алгоритм Флойда более общий, поскольку он позволяет одновременно найти минимальные пути между любыми двумя узлами сети.

Алгоритм Дейкстры. В процессе выполнения этого алгоритма при переходе от Узла i к следующему узлу / используется специальная процедура пометки ребер. Обозначим через и, кратчайшее расстояние от исходного узла 1 до узла i, через dtj - длину ребра (г, j). Тогда для узла / определим метку [ujt i] следующим образом.

[Uj, i] = [ut + dh, i],d(/>0

Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Временная метка впоследствии может быть заменена на другую временную, если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус временной метки изменяется на постоянный.

Вычислительная схема алгоритма состоит из следующих этапов.

Этап 0. Исходному узлу (узел 1) присваивается постоянная метка [0, -]. Полагаем i = 1.

Этап 1.

а) Вычисляются временные метки [и1 + dtj, i] для всех узлов у, которые можно достичь непосредственно из узла I и которые не имеют постоянных ме-