ток. Если узел уже имеет метку [и, k], полученную от другого узла k, и, если ut + dtj < ujt тогда метка [uy, k] заменяется на \ul + dtj, i],

b) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка [ur, s] с наименьшим значением расстояния иг среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = г и повторяем этап i.

Пример 6.3.4

На рис. 6.14 показана транспортная сеть, состоящая из пяти городов (расстояния между городами (в милях) приведены возле соответствующих дуг сети). Необходимо найти кратчайшие расстояния от города 1 (узел 1) до всех остальных четырех городов.

Временный статус метки [40, 3] узла 4 заменяется постоянным (ut = 40).

Этап 3. Из узла 4 можно достичь узлов 2 и 5. После вычисления меток получим следующий их список.

Узел Метка Статус метки

1 [0, -] Постоянная

2 [40 + 15, 4] = [55, 4] Временная

3 [30,1] Постоянная

4 [40,3] Постоянная

5 [90, 3] или [40 + 50, 4] = [90, 4] Временная

Временная метка [100, 1], полученная узлом 2 на втором этапе, изменена на [55, 4]. Это указывает на то, что найден более короткий путь к этому узлу (проходящий через узел 4). На третьем этапе узел 5 получает две метки с одинаковым значением расстояния иь = 90.

Этап 4. Из узла 2 можно перейти только в узел 3, но он уже имеет постоянную метку, которую нельзя изменить. Поэтому на данном этапе получаем такой же список меток, как и на предыдущем, но с единственным изменением: метка узла 2 получает статус постоянной. С временной меткой остается только узел 5, но, так как из этого узла нельзя попасть ни в какой другой, процесс вычислений заканчивается.

Алгоритм позволяет проводить вычисления непосредственно на схеме сети, как показано на рис. 6.15.

[55,4](3)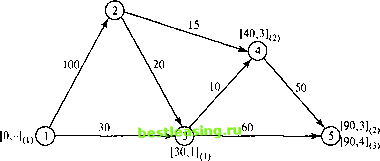

() = шаг

Рис. 6.15. Применение алгоритма Дейкстры

Кратчайший маршрут между узлом 1 и любым другим узлом определяется начиная с узла назначения путем прохождения их в обратном направлении с помощью информации, представленной в постоянных метках. Например, для определения кратчайшего маршрута между узлами 1 и 2 получаем такую обратную последовательность узлов

(2) -> [55, 4] -> (4) -> [40, 3] -> (3) -> [30, 1] -> (1). Таким образом, получаем путь 1 -> 3 -> 4 -> 2 общей длиной 55 миль.

Программа TORA также может применять алгоритм Дейкстры для решения сетевых задач. Для этого в меню SOLVE/MODIFY выберите команду Solve problem Iterations1 Dijkstras algoritm (Алгоритм Дейкстры). На рис. 6.16 показано выходное окно TORA с решением задачи из примера 6.3.4 (файл ch6ToraDijkstraEx6-3-4.txt).

TV* II WoifcMo ..Fdr-IMTlMOifati-.t.t. I 4 I.I

NETWOHK MCIDEIS

Рис. 6.16. Решение задачи из примера 6.3.4

УПРАЖНЕНИЯ 6.3.2

1. На рис. 6.17 показана транспортная сеть, соединяющая восемь городов, и расстояния между ними. Найдите кратчайшие маршруты между следующими городами.

a) Города 1 и 8.

b) Города 1 и 6.

c) Города 4 и 8.

d) Города 2 и 6.

2. Найдите кратчайшие пути между узлом 1 и всеми остальными узлами сети, представленной на рис. 6.18.

3. Найдите оптимальное решение задачи из упражнения 6.3.1.1.

4. Найдите оптимальное решение задачи из упражнения 6.3.1.2.

5. Найдите оптимальное решение задачи из упражнения 6.3.1.4.