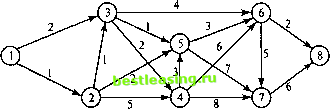Рис. 6.17. Сеть для задачи из упражнения 1 6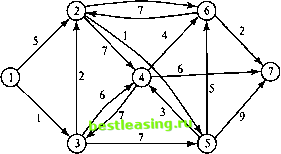

Рис. 6.18. Сеть для задачи из упражнения 2

Алгоритм Флойда. Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с п строками и п столбцами. Элемент (£, /) равен расстоянию dtj от узла i к узлу /, которое имеет конечное значение, если существует дуга (i, j), и равен бесконечности в противном случае.

Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k и заданы расстояния между ними (рис. 6.19). Если выполняется неравенство dtj + djk < dllt, то целесообразно заменить путь i -> k путем i->;->ft. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.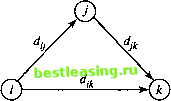

Рис. 6.19. Треугольный оператор Флойда Алгоритм Флойда требует выполнения следующих действий.

Этап 0. Определяем начальную матрицу расстояний D0 и матрицу последовательности узлов S0. Диагональные элементы обеих матриц помечаются знаком - , показывающим, что эти элементы в вычислениях не участвуют. Полагаем k = 1.

1 2 ... j ... п

1 2 ... j ... л

So =

Основной этап к. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения треугольного оператора ко всем элементам dtj матрицы Dk r Если выполняется неравенство

dik + dkj < d,j> (i*k,j*kni*j), то делаем следующее:

a) создаем матрицу Dk путем замены в матрице Dk 1 элемента dtj суммой dlk + dkj,

b) создаем матрицу Sk, меняя в матрице S4 j элемент s, на h. Полагаем k = k + 1 и повторяем этап ft.

Поясним действия, выполняемые на k-м этапе алгоритма, представив матрицу Dk j так, как она показана на рис. 6.20. На этом рисунке строка k и столбец k являются ведущими. Стро-ка i- любая строка с номером от 1 до А - 1, а строка р - произвольная строка с номером от k + 1 до л. Аналогично столбец / представляет любой столбец с номером от 1 до k - 1, а столбец q - произвольный столбец с номером от k + 1 до л. Треугольный оператор выполняется следующим образом. Если сумма элементов ведущих строки и столбца (показанных в квадратиках) меньше элементов, находящихся на пересечении столбца и строки (показаны в кружках), соответствующих рассматриваемым ведущим элементам, то расстояние (элемент в кружке) заменяется суммой расстояний, представленных ведущими элементами.

После реализации л этапов алгоритма определение по матрицам Dn и Sn кратчайшего пути между узлами i и j выполняется по следующим правилам.

1. Расстояние между узлами i и j равно элементу dtJ в матрице Dn.

2. Промежуточные узлы пути от узла i к узлу j определяем по матрице Sn. Пусть s0 = k, тогда имеем путь i -> k -> /. Если далее slk = k и skj = j, тогда считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла i к узлу k и от узла k к узлу

Столбец j

Строка i

Ведущая строка

Строка р

Ведущий столбец

Столбец Q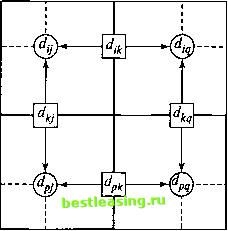

Рис. 6.20. Реализация треугольного оператора

Пример 6.3.5

Найдем для сети, показанной на рис. 6.21, кратчайшие пути между любыми двумя узлами. Расстояния между узлами этой сети проставлены на рисунке возле соответствующих ребер. Ребро (3, 5) ориентированно, поэтому не допускается движение от узла 5 к узлу 3. Все остальные ребра допускают движение в обе стороны.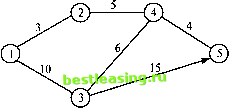

Рис. 6.21. Сеть для примера 6.3.5

ЭтапО. Начальные матрицы D0 и S0 строятся непосредственно по заданной схеме сети. Матрица D0 симметрична, за исключением пары элементов и d53, где d63 = ос (поскольку невозможен переход от узла 5 к узлу 3).