Этап 1. В матрице D0 выделены ведущие строка и столбец с номером k = 1.

Затемненными представлены элементы d23 и d32, единственные среди элементов матрицы D0, значения которых можно улучшить с помощью треугольного оператора. Таким образом, чтобы на основе матриц D0 и S0 получить матрицы D, и Sv выполняем следующие действия.

1. Заменяем d23 на d2X + dl3 = 3 + 10 = 13 и устанавливаем s23 = 1.

2. Заменяем d32 на d3l + dl2 = 10 + 3 = 13 и устанавливаем s32 = 1. Матрицы D, и S, имеют следующий вид.

Этап 2. Полагаем k = 2; в матрице D; выделены ведущие строка и столбец. Треугольный оператор применяется к элементам матриц D, и выделенным затенением. В результате получаем матрицы D2 и S2.

Этап 3. Полагаем k = 3; в матрице D2 выделены ведущие строка и столбец.

Треугольный оператор применяется к затемненным элементам матриц D2 и S2. В результате получаем матрицы D3 и S3.

Этап 4. Полагаем k = 4, ведущие строка и столбец в матрице D3 выделены. Получаем новые матрицы Dt и S4.

Этап 5. Полагаем k - 5, ведущие строка и столбец в матрице Б4 выделены.

Никаких действий на этом этапе не выполняем; вычисления закончены.

Конечные матрицы £>4 и St содержат всю информацию, необходимую для определения кратчайших путей между любыми двумя узлами сети. Например, кратчайшее расстояние между узлами 1 и 5 равно diS = 12.

Для определения соответствующих маршрутов напомним, что сегмент маршрута (i,j) состоит из ребра (/, /) только тогда, когда stj = j. В противном случае узлы i и j связаны, по крайней мере, через один промежуточный узел. Например, поскольку s,5 = 4 и siS = 5, сначала кратчайший маршрут между узлами 1 и 5 будет иметь вид 1 - 4 - 5. Но так как д-,4 ф 4, узлы 1 и 4 в определяемом пути не связаны одним ребром (но в исходной сети они могут быть связаны непосредственно). Далее следует определить промежуточный узел (узлы) между первым и четвертым узлами. Имеем su - 2 и s2i = 4, поэтому маршрут 1 - 4 заменяем 1 - 2 -> 4. Поскольку д-,2 = 2 и$24 = 4, других промежуточных узлов нет. Комбинируя определенные сегменты маршрута, окончательно получаем следующий кратчайший путь от узла 1 до узла 5:1- 2- 4- 5. Длина этого пути равна 12 милям.

Программа TORA также может применять алгоритм Флойда для решения сетевых задач. Для этого в меню SOLVE/MODIFY выберите команду Solve problem Iterations Floyds algoritm (Алгоритм Флойда). На рис. 6.22 показано выходное окно TORA с решением задачи из примера 6.3.5 (файл ch6ToraFloydEx6-3-5.txt).

УПРАЖНЕНИЯ 6.3.3

1. В задаче из примера 6.3.5 определите кратчайшие пути между следующими парами узлов.

a) От узла 5 к узлу 1.

b) От узла 3 к узлу 5.

c) От узла 5 к узлу 3.

d) От узла 5 к узлу 2.

2. Примените алгоритм Флойда к сети, показанной на рис. 6.23. Заметьте, что ребра (7, 6) и (6, 4) ориентированы. Определите кратчайшие пути между следующими парами узлов.

- TORA D:\Work\ToraFiles\ch6ToraFloydEx6 ЗЪ.Ы

то ид орт, Ли i i .mh- ид -и \ш ripii. Аичпаш на

NETWORK MODELS

FLOYu S SHORTEST ROUTE ALGuRITHM Select Output Option

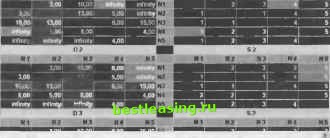i°uc. 6.22. Решение задачи из примера 6.3.5

a) От узла 1 к узлу 7.

b) От узла 7 к узлу 1.

c) От узла 6 к узлу 7.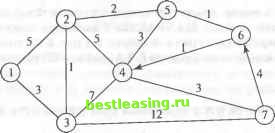

Рис. 6.23. Сеть для задачи из упражнения 2

3. Телефонная компания обслуживает шесть удаленных друг от друга районов, которые связаны сетью, показанной на рис. 6.24. Расстояния на схеме сети указаны в милях. Компании необходимо определить наиболее эффективные маршруты пересылки сообщений между любыми двумя районами.