Применение описанной процедуры к задаче данного примера приводит к следующей задаче линейного программирования, которая уже имеет структуру сетевой модели.

Таким образом, задачу распределения рабочих можно представить в виде эквивалентной задачи вычисления потока минимальной стоимости в сети с ограниченной пропускной способностью (рис. 6.40). Поскольку здесь не налагаются ограничения на верхние границы пропускных способностей, эту задачу можно также решить как транспортную задачу (см. раздел 5.5).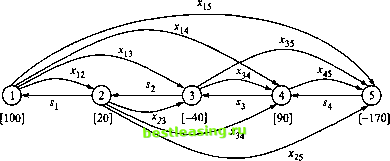

Рис. 6.40. Сеть для примера 6.5.3

УПРАЖНЕНИЯ 6.5.2

1. Сформулируйте задачу линейного программирования, минимизирующую стоимость потока в сети, показанной на рис. 6.41, до и после исключения нижних границ пропускных способностей дуг.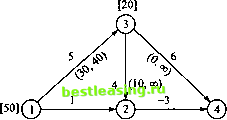

(0, да) (10, оо)

[-40]

Рис. 6.41. Сеть для задачи из упражнения 1

2. С помощью непосредственной проверки найдите допустимое решение задачи определения потока минимальной стоимости в модели распределения рабочих из примера 6.5.3 (см. рис. 6.40). Интерпретируйте найденное решение в терминах первоначальной постановки задачи (как количество нанимаемых рабочих), проверьте выполнение ограничений модели и найдите соответствующую общую стоимость.

3. Переформулируйте задачу распределения рабочих (пример 6.5.3), предполагая, что рабочие нанимаются не менее, чем на два месяца. Запишите соответствующую задачу линейного программирования и преобразуйте ее в задачу определения потока минимальной стоимости в сети с ограниченной пропускной способностью.

4. Сформулируйте задачи ЛП и соответствующие задачи определения потока минимальной стоимости для модели распределения рабочих из примера 6.5.3, используя следующие данные о потребностях рабочих в течение последующих пяти месяцев. Стоимость найма одного рабочего в эти месяцы составит соответственно 50, 70, 85, 100 и 130 долл.

5. Преобразование сети с ограниченной пропускной способностью в сеть с неограниченной пропускной способностью. Покажите, что дугу (i -> j) с ограниченным потоком xtj<ult можно заменить двумя дугами, не имеющими ограничений на величину потока, - (i -> k) и (k - j) с результирующим (выходным) потоком [-и ] в узле k и дополнительным (входным) потоком [+и:/] в узле у. В результате сеть с ограниченной пропускной способностью преобразуется Тв сеть с неограниченной пропускной способностью, т.е. в транспортную модель (раздел 5.1). Примените описанное преобразование к сети на рис. 6.42 и найдите оптимальное решение полученной транспортной задачи с помощью программы TORA.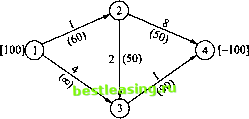

Рис. 6.42. Сеть для задачи из упражнения 5

6.5.3. Симплексный алгоритм для сетей с ограниченной пропускной способностью

Предлагаемый алгоритм повторяет в точности те же этапы, что и обычный симплекс-метод. Вместе с тем здесь учитывается специальная структура сетевой модели. Используя определения из раздела 6.5.2, где /, - результирующий поток через

узел i, строим симплексный алгоритм на основе условия =0 . Это условие оз-

начает, что в сети суммарный объем предложений равен суммарному объему спроса. Мы всегда можем удовлетворить данное условие, введя фиктивный источник или сток, которые можно связать с остальными узлами сети дугами с нулевой стоимостью и бесконечной пропускной способностью. Однако сбалансированность сети не гарантирует существования допустимого решения, поскольку этому может воспрепятствовать ограниченность пропускных способностей дуг.

Опишем алгоритм нахождения потока минимальной стоимости для сетей с ограниченной пропускной способностью. Отметим, что он базируется на стандартном симплекс-методе и теории двойственности (главы 3 и 4). Здесь также полезно знакомство с симплекс-методом для задач ЛП с ограниченными переменными (раздел 7.3).

ШагО. Определяем для данной сети начальное базисное допустимое решение (множество дуг). Переходим к шагу 1.

Шаг 1. С помощью условия оптимальности симплекс-метода определяем вводимую в базис переменную (дугу). Если на основе условия оптимальности определяем, что последнее решение оптимально, вычисления заканчиваются. В противном случае переходим к шагу 2.

Шаг 2. На основе условия допустимости симплекс-метода определяем исключаемую из базиса переменную (дугу). Изменив базис, возвращаемся к шагу 1.

Сети с п узлами и нулевым результирующим потоком (т.е. при выполнении равенства Д + f2 + ... + fn = 0) соответствуют п - 1 независимым ограничениям в виде равенств. Поэтому базисное решение должно содержать п - 1 переменных. Можно показать, что базисное решение соответствует остовному дереву данной сети (см. раздел 6.2).

Вводимая переменная (дуга) на шаге 1 определяется путем вычисления разностей ztj - ctj для всех текущих небазисных дуг (t, j). Если для всех разностей z - ctj< 0, тогда текущее базисное решение оптимально. Иначе в качестве вводимой в базис переменной выбираем дугу, которой соответствует наибольшее положительное значение разности гц - сц.

Вычисление разностей ztj - сц основано на соотношениях двойственности точно так же, как в транспортной модели (см. раздел 5.3.4). Обозначим через wt переменную задачи, двойственной к задаче ЛП (определенной в разделе 6.5.2), которая (переменная) соответствует ограничению узла /. Тогда данная двойственная задача формулируется следующим образом.

Максимизировать z = £/wi

при выполнении условий

w,-w< сц, (/, у) е А,

переменные wt произвольного знака (i = 1, 2, п).

Из теории линейного программирования следует, что wt - w = с для любой базисной дуги (/, j). Поскольку исходная задача ЛП (раздел 6.5.2) по определению